This Might Get Messy

Welcome to my little corner of the baseball world. This year, I’m going to attempt to publish my thoughts on a semi-weekly basis of a few different baseball metrics. These are not your normal baseball metrics. They’re purely out of my head, and as far as I can tell, they’ve never been measured before. I won’t jump into the formulas for each here, and instead will try to provide a bit of narrative around each so that you know what you’re looking at.

Exciting Game Index (EGI)

The origin of the Exciting Game Index (EGI) is the 2008 ALCS. As a Red Sox fan, I was especially tuned into the series. Game 5 was particularly riveting. Let me remind you: the Rays were beating the Red Sox 3 games to 1 and jumped out to a early lead of 5-0 against Daisuke Matzusaka. By the 4^th inning, the game, the series, the season, looked over for the Red Sox. When the Rays piled on to make it 7-0 in the 7^th inning, the Red Sox staff was probably taping up plastic in the Rays visiting clubhouse. And then something funny happened: the Red Sox won the game. Mind you, this isn’t a feel good Red Sox story (cf. 2004): the Red Sox lost this series in 7 games. However, there were few people that would doubt that Game 5 was a very exciting game to watch. A huge, improbable comeback finishing with a walk off win in the playoffs? This is why we watch baseball.

Statistically, it’s not hard to quantify the Red Sox chances of coming back from a 7-0 deficit with 2 outs in the 7^th inning. It’s less than 1%. Here’s what happens when you graph the Red Sox win expectancy in that game: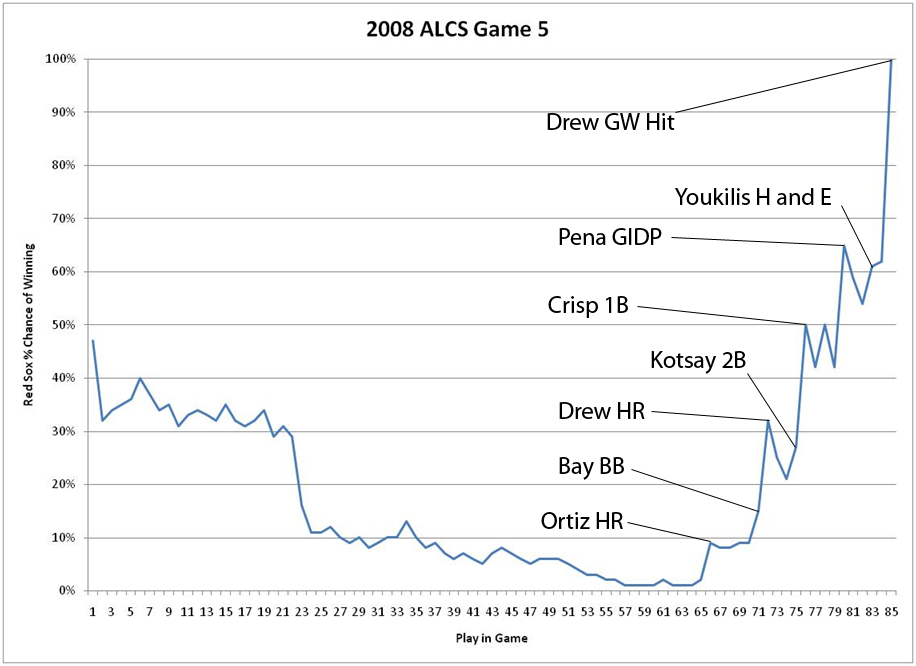

What if the Red Sox had lost that game after coming all the way back? No matter, it still would have been exciting to the casual baseball observer without a rooting interest. I reasoned that it wasn’t necessarily the outcome of the game that mattered, but how we got there. No one doubts that a 7-0 game is a laugher, and relatively boring, or that a 1-0 game is going to be exciting to watch all the way through. But, we’ve all see boring 3-0 games, where one team just dominates the other for 9 innings. That’s no fun either. What matters is the high leverage situations that teams put themselves into. A 1-0 game where the bases are loaded every inning but no one can manage to score is inherently more exciting than a 1-0 game that neither team can manage to get on base.

In an attempt to measure this, EGI was born. As it turns out, Game 5 a very exciting game when compared to other games in post season history. From 1985-2008, it was the 6th most exciting ALCS game.

The improbable 2011 World Series gave me renewed interest in measuring this. Certainly playoffs series are fun to compare against each other, but most baseball fans are watching them anyway. It makes more sense to measure the regular season, to figure out which games are worth watching. That’s exactly what I’ll attempt to do on a weekly basis.

Each Thursday, I’ll publish my list of most exciting games, as well as a detailed ranking of all the games for the week. I’ll keep a running tab as to which teams are the most exciting, and attempt to predict the weekend games so hopefully we have a good idea which to tune into.

Later in the season, I’ll jump into the metric itself and show how it’s calculated.

Streak Factor

In 2010, some friends were debating the outcome of the upcoming ALCS (Rangers vs. Yankees). One friend noted that the Rangers could win because they beat up the Yankees in August and that the Yankees seemed to be “really streaky this year.” The other friend noted that he didn’t think this was accurate and went about trying to prove it. His initial thought was to try to develop a way to measure streakiness. His initial thought was a good one: take all the streaks that a team experienced throughout the year and figure out how long the average streak should be.

First, a bit of math (a more detailed analysis will follow at a later date). SF is a pure calculation of the average length of a streak across the season. For instance, a team that wins every other game ends up with 162 1-game streaks. This means their SF is a perfect 1.000. A team that wins all 162 games and loses none has one 162-game streak. Their SF is a perfect 162.000. SF is bounded by 1.000 and 162.000, we don’t expect any teams to approach either limit, in the same way that no one gets a 4.000 SLG or a 1.000 OBP for an entire season.

Streak Factor was born. An important qualification here is that a very good team or a very bad team will have a lot of streaks. There’s going to win a lot or lose a lot. A .500 team shouldn’t have nearly as many streaks. If they do, we will consider them streaky.

SF is measured specifically against the expected SF (eSF) of a team. The eSF is a function of winning percentage. For a .500 team, eSF is 2.000. What this means is that we expect a .500 team to have on average a 2 game winning (or losing streak) before reverting to their (.500) mean. Therefore, if a .500 team notches a 7 game winning streak, we would expect them to trade wins and losses (several 1 game streaks) to get their average streak back to 2.000.

Subtracting eSF from SF yields SFDiff. If a team ends up with a positive SFDiff, we’ll consider the team “streaky.” If a team ends up with a negative SFDiff, then we’ll consider the team “consistent.” Let’s take a look at an example.

The 2001 Mariners SF was 2.531. At first glance, this seems exceptionally high. It means that the Mariners won (or lost) their games in clumps – on average, 2.5 per clump. Over the last 10 years, this is actually one of the 5 highest Streak Factors. However, you should remember that the 2001 Mariners actually hold the record for most regular season wins (116). For a team with a .716 WinPct, the eSF is 2.476. Subtracting eSF from SF yield SFDiff of .055. Therefore, we can conclude, the 2001 Seattle Mariners, while a very good team and significantly more streaky than many other teams, are averagely streaky compared to other hypothetical .716 WinPct teams.

Let’s look at one more team, on the opposite side of the spectrum. The 2002 Blue Jays were a .481 team, and they had a SF of 2.571, this is essentially the same as the 2001 Mariners, who won far more games. The eSF for a .481 team is 2.002. SFDiff = 2.571 – 2.002 = .569. They didn’t have a very long winning or losing streak by historical standards (7 game winning streak, 9 game losing streak), but they had a ton of 4, 5, 6 game streaks, both winning and losing. In fact, they only had 22 one game streaks the entire season. In the last 10 years, the 2002 Blue Jays are listed as the streakiest team compared to eSF.

On Sundays, we’ll take a look at all 30 teams and try to understand who is streaky and who is consistent. Utilizing this, we might get a good idea which teams are likely to continue their streaks, and make some predictions about the week ahead.

There’s a lot more analysis behind this, that I’ll publish at a future date, but roughly speaking, more consistent teams tend to go to the playoffs more frequently and do better once they get there.