What is EGI?

The origin of the Exciting Game Index (EGI) is the 2008 ALCS. Game 5 was particularly riveting. Let me remind you: the Rays were beating the Red Sox 3 games to 1 and jumped out to a early lead of 5-0 against Daisuke Matzusaka. By the 4^th inning, the game, the series, the season, looked over for the Red Sox. When the Rays piled on to make it 7-0 in the 7^th inning, the Red Sox staff was probably taping up plastic in the Rays visiting clubhouse. And then something funny happened: the Red Sox won the game. Mind you, this isn’t a feel good Red Sox story (cf. 2004): the Red Sox lost this series in 7 games. However, there were few people that would doubt that Game 5 was a very exciting game to watch. A huge, improbable comeback finishing with a walk off win in the playoffs? This is why we watch baseball.

Statistically, it’s not hard to quantify the Red Sox chances of coming back from a 7-0 deficit with 2 outs in the 7^th inning. It’s less than 1%. Here’s what happens when you graph the Red Sox win expectancy in that game: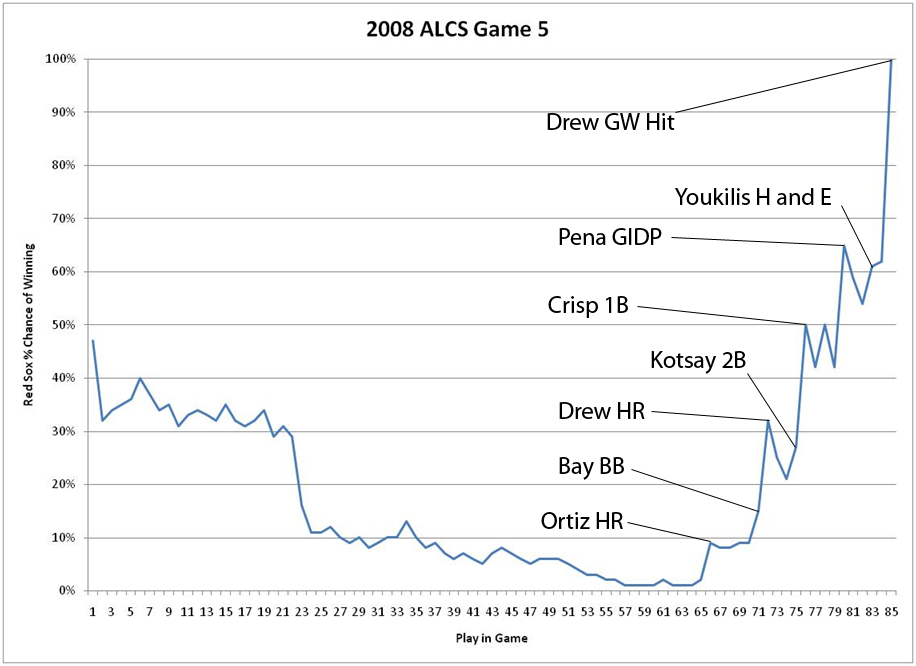

What if the Red Sox had lost that game after coming all the way back? No matter, it still would have been exciting to the casual baseball observer without a rooting interest. I reasoned that it wasn’t necessarily the outcome of the game that mattered, but how we got there. No one doubts that a 7-0 game is a laugher, and relatively boring, or that a 1-0 game is going to be exciting to watch all the way through. But, we’ve all see boring 3-0 games, where one team just dominates the other for 9 innings. That’s no fun either. What matters is the high leverage situations that teams put themselves into. A 1-0 game where the bases are loaded every inning but no one can manage to score is inherently more exciting than a 1-0 game that neither team can manage to get on base.

In an attempt to measure this, EGI was born. As it turns out, Game 5 a very exciting game when compared to other games in post season history. From 1985-2008, it was the 6th most exciting ALCS game.

EGI averages 33, and ranges between 8-75. Anything above 65 is a top 2% game.

Here’s the formula: the sum of all win expectancy changes divided by the total number of plays, multiplied by 1000.